Pythagorean Theorem Calculator
Example: If a=3 and b=4, then c=√(3² + 4²)=5
2. Leg (a or b): a² = c² - b² or b² = c² - a²
Example: If b=4 and c=5, then a=√(5² - 4²)=3
3. Angles:
- ∠α = arcsin(a/c) or arcsin(b/c)
- ∠β = 90° - ∠α
Example: For a=3, c=5: ∠α=arcsin(3/5)≈36.87°
4. Area: (a × b)/2
Example: For a=3, b=4: area=(3×4)/2=6
5. Perimeter: a + b + c
Example: For a=3, b=4, c=5: perimeter=3+4+5=12
6. Height (h): (a × b)/c
Example: For a=3, b=4, c=5: h=(3×4)/5=2.4
The Pythagorean Theorem is a foundational rule in geometry that connects the three sides of a right-angled triangle. This type of triangle features one angle that is exactly 90 degrees. The theorem explains how the length of the hypotenuse (the longest side, opposite the right angle) relates to the other two sides.
Understanding the Pythagorean Theorem
According to the theorem:
a² + b² = c²
Where:
aandbare the lengths of the two shorter sidescis the length of the hypotenuse
This relationship allows you to find any side of a right triangle if the other two sides are known.
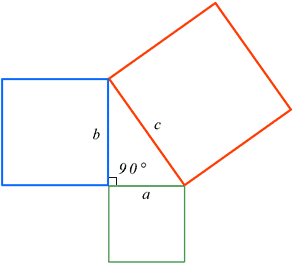
Example: Solving for the Hypotenuse
If you know that:
a = 3
b = 4
Then:
c = √(a² + b²)
c = √(3² + 4²)
c = √(9 + 16)
c = √25 = 5
So, the hypotenuse is 5 units long.
Solving for a or b (a Missing Short Side)
If you’re given the hypotenuse (c) and one leg (a or b), you can rearrange the formula:
a = √(c² – b²)
b = √(c² – a²)
This flexibility makes the Pythagorean Theorem very helpful in construction, navigation, architecture, and many areas of science and engineering.
Geometric Insights and Proofs
The Pythagorean Theorem is one of the most proven concepts in mathematics, with hundreds of demonstrations from different fields.
Algebraic Proof Using Squares
There are two popular visual proofs that use squares and triangle arrangements:
Proof 1: Square Built from Right Triangles
In the first proof, four identical right triangles are arranged around a central square with side c. This creates a larger square with total side length (a + b).
Area of large square = (a + b)²
Area of 4 triangles = 4 × (½ × a × b) = 2ab
Area of center square = c²
So:
(a + b)² = c² + 2ab
Rearranged:
c² = (a + b)² – 2ab = a² + b²
Proof 2: Square Within a Square
In another arrangement, the same four triangles are organized differently to form a smaller inner square with side (b - a) and a large outer square with side c.
Area of inner square = (b – a)²
Area of 4 triangles = 2ab
Total area = c²
So:
c² = (b – a)² + 2ab = a² + b²
Both setups arrive at the same conclusion:
c² = a² + b²
More Than One Way to Prove It
While the two algebraic proofs above are simple and easy to visualize, there are many other ways to prove the Pythagorean Theorem. These include:
Geometric proofs
Calculus-based proofs
Coordinate geometry
Visual and interactive models
Why It Matters
The Pythagorean Theorem is not only a critical concept in school math but also an essential tool in real-world applications like:
Measuring distances
Designing buildings
Mapping and GPS systems
Physics and engineering
This calculator helps you quickly find a missing side of a right triangle by applying the theorem instantly—perfect for students, teachers, and professionals alike.
