Triangle Calculator

A triangle is a fundamental geometric shape formed by three straight lines connecting three points (called vertices). Each triangle has three interior angles and three sides. Triangles appear everywhere in math, architecture, physics, and everyday life. This triangle calculator helps you solve any triangle based on your input—whether you’re given sides, angles, or a mix of both.

It provides instant solutions for:

• Missing side lengths or angles

• Triangle area

• Triangle type classification

• Medians, inradius, circumradius

• And more, using the Law of Sines, Law of Cosines, Heron’s Formula, and the Pythagorean Theorem.

 Understanding Triangle Types

Triangles can be classified in two ways: by their sides and by their angles.

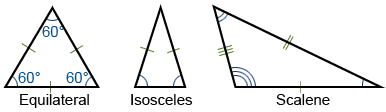
By Sides:

• Equilateral Triangle: All three sides and angles are equal (each angle is 60°).

• Isosceles Triangle: Two sides are equal, and the angles opposite them are also equal.

• Scalene Triangle: All sides and all angles are different.
  

 By Angles:

• Right Triangle: Has one 90° angle. The longest side (opposite the right angle) is called the hypotenuse.

• Acute Triangle: All angles are less than 90°.

• Obtuse Triangle: Has one angle greater than 90°.
  

Equal parts in diagrams are often marked with tick marks or arcs. Remember, the drawings are for reference only and not to scale.

Triangle Rules You Must Know

• The sum of the interior angles of any triangle is always 180 degrees.

• An exterior angle equals the sum of the two opposite interior angles.

• Triangle Inequality Theorem: The sum of any two sides must be greater than the third side. Otherwise, a triangle cannot exist.

These basic properties are essential for solving triangles correctly.

 Pythagorean Theorem (For Right Triangles Only)

This famous formula relates the sides of a right triangle:

       a² + b² = c²

Where:

• a and b are the legs

• c is the hypotenuse (the side opposite the right angle)

Example: If a = 3 and c = 5,
then:

     3² + b² = 5² → 9 + b² = 25 → b² = 16 → b = 4

This formula only works with right triangles.

Law of Sines – Solve Any Triangle

Use when you know either:

• Two angles and one side (AAS or ASA)

• Two sides and one non-included angle (SSA)

Formula:

     a / sin(A) = b / sin(B) = c / sin(C)

Example: Given side b = 2, ∠B = 90°, and ∠C = 45°
You can find side c:

  2 / sin(90°) = c / sin(45°) → c = 2 × sin(45°) = √2

This method works for both right and oblique triangles.

Law of Cosines – When You Know All 3 Sides or SAS

Used when:

• You know all 3 sides (SSS)

• You know 2 sides and the included angle (SAS)
  
  To find angle A:
  A = arccos((b² + c² – a²) / 2bc)

Example: a = 8, b = 6, c = 10

B = arccos((64 + 100 – 36) / 160) = arccos(0.8) ≈ 36.87°

 Triangle Area – Choose Your Method

1. Base × Height

     Area = ½ × base × height

Example: b = 5, h = 6 → Area = 15

2. Two Sides and the Included Angle

    Area = ½ × a × b × sin(C)

Example: a = 9, b = 7, ∠C = 30° → Area ≈ 15.75

3. Heron’s Formula (When You Know All 3 Sides)

     s = (a + b + c) / 2
    Area = √[s(s – a)(s – b)(s – c)]

Example: a = 3, b = 4, c = 5 → s = 6

Area = √(6×3×2×1) = √36 = 6

 Triangle Medians

A median is a line from a vertex to the midpoint of the opposite side.

To calculate the median from vertex A:

    ma = ½ × √(2b² + 2c² − a²)

All three medians intersect at the centroid, which is the triangle’s center of gravity and balances the triangle if made from a uniform material.
   

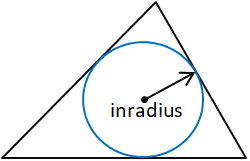
 Inradius – Circle Inside the Triangle

The inradius is the radius of a circle perfectly inside the triangle, touching all three sides.

    s = (a + b + c) / 2
    Inradius = Area / s

This is useful in design and architecture when fitting shapes within constraints.
   

Circumradius – Circle Through Triangle Vertices

The circumradius is the radius of a circle that passes through all three vertices of the triangle.

Formula:

    Circumradius = a / (2 × sin(A))

 

This is often used in navigation, astronomy, and trigonometric modeling.
     

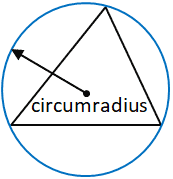
(Any side and its opposite angle can be used.)

This triangle calculator helps you compute sides, angles, area, medians, and radius values using built-in formulas. Whether you’re solving for a right triangle or using trigonometry, it’s a helpful tool for students, teachers, and professionals.